如何提高Python运行效率

Python为什么慢

由于 Python 是一种高级的动态语言，它的代码在运行的时候才会进行编译，而且编译过程中进行了非常多的复杂的工作，例如，Python的语法大大简化了变量的声明，它不需要指定变量的类型，因此在运行的时候解释器需要推断变量的类型，这样就会耗费更多的时间。

简而言之，python之所以能让你写的很轻松，是因为他自己在背后负重前行。

除了使用低级语言，有什么可以先试试的办法？

当你发现你使用了for循环并且迭代次数很大的时候，你就要开始考虑了，这个过程能否用矩阵运算来替代？

Python初学者或者线性代数新手可能会不太了解矩阵，说白了其实就是把数字摆成方阵，然后同时进行相同方式的运算处理，而这些运算处理有非常多花里胡哨的名堂，这就是线性代数的范畴了。但是在这里，并不需要线性代数的知识。Numpy是一个非常强大的Python包，它可以帮助你快速地实现矩阵运算。它之所以快是因为它在底层用C语言做了非常多的优化，其中最重要的是它能够进行并行计算，充分发挥机器的性能，而我们直接用Python的for循环是串行的，也就是要等上一个计算完成后才能开始下一个，在数据量巨大的时候，这个速度简直是灾难性的。

当然并不是所有的循环逻辑都能用矩阵运算来替代，比如，在使用for循环来对不同api进行请求时，这个循环逻辑里包含了数值计算之外的操作，因此不能用矩阵运算来替代。但是，如果你能够抽象出一个纯数值计算的循环，比如在这个例子里，假如能使api一次性返回所有数据，那么你可以把数据写入一个矩阵，就可以使用矩阵运算来并行处理数据了。

一个例子：用三维坐标系展示四维数据

我曾经对四维空间非常感兴趣，从数学上来说，四维空间是确确实实存在的，但是我知道我们无法在三维空间里直接显示四维的物体，所以我想，至少可以想些办法，仅仅是把数据表现出来，这样就可以更好地让我们理解四维空间的存在。一个很好的办法就是，在一个三维图像中，使用渐变颜色来表示第四维度的数据。

于是我没多想，随便写了下，用了很多嵌套for循环，

可以看到，我甚至写了一个生成器oscillate_range来优化这个过程，试图减少一些多余的循环次数。我使用tqdm模块来显示最外层循环的进度条。

可以看到，在最初的几个循环速度不能说快，但还是可以接受的，但是在接近末尾的循环中，速度就令人窒息了。这其实是因为相同的采样精度下，半径越小，球体内的数据点越少，反之，半径越大，球体内的数据点越多，运算时间就越长了。回想起来我最初跑这个代码的时候，只是创建一个球体而已，上了个大号厕所回来还没跑完，这是python的性能第一次切切实实的影响到了我的心情。所以我觉得一定有更好的实现方法，于是才有了下面的故事。

使用timeit模块进行计时

可以看到，仅仅使用了一个meshgrid函数，就完成了上面的层层嵌套for循环的工作。而且并行运算的速度快了好几个数量级，根本不需要去管计算顺序了。

总结

虽然矩阵版本的代码看起来更简单，但是这个meshgrid函数在背后做了非常多的工作，远比我们自己写的浅显直观的嵌套循环的逻辑代码要复杂得多。

另外，我相信很多Python的初学者肯定也听说过各路大佬吐槽Python速度慢之类的问题，因此在开始写代码的时候就在担心怎么搞优化提速之类的问题，但其实只有当你切身体会到了那种痛，你才会需要去想办法解决，而且你自然而然会找到正确的优化方向。既然你都选择了Python，那么只需要把握好写代码的第一原则，能用就行。

被遗忘的四维球体

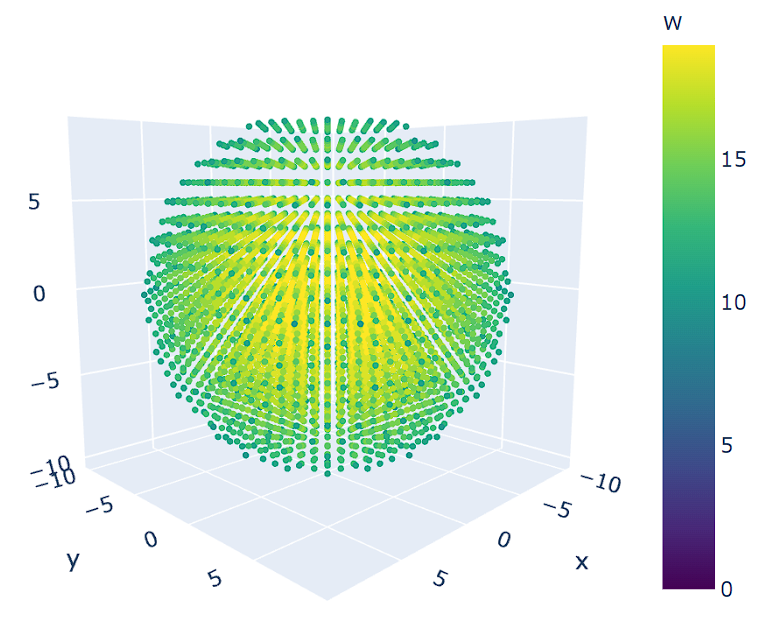
这并不是一个真正的四维球体，只是一个用颜色渐变来标记数据点在第四维度的位置到球心距离大小的三维球体。也可以说这个三维球体是四维球体在我们这片三维空间中的投影。从图中可以得出，越靠近球心，第四维度的数值越大。因此，可以合理地想象，当一个四维球体被向我们的这片三维空间均匀挤压，假设挤压不会导致三维球体发生形变，那么这个球体会从中心开始密度变大。那么如果最终导致形变，从三维看来，物质会从球心开始向外膨胀。用三体的话来说，正如二向箔让三维空间向二维跌落时，二维空间会向平面四周扩散，我们这个“三向砖”，能让四维空间向三维跌落，这个三维空间就会向各个方向扩散。同时，正如三体中对四维空间的形容，从四维角度看三维，所有结构都是展开的。我们的三维球体模型内部，许多第四维度上的物质相当于是凭空出现在了我们的三维空间中，才导致了我们球体的膨胀。